Binary Classification
Logistic regression is an algorithm for binary classification.
Logistic Regression
[latex]\hat{y} = w^Tx + b[/latex] : An algorithm that can output a prediction. More formally, you want [latex]\hat{y}[/latex] to be the probability of the chance. And [latex]\hat{y}[/latex] should really be between zero and one. sigmoid : [latex]\sigma (z) = \frac {1}{1 + e^{-z}}[/latex]
Logistic Regression Cost Function
To train the parameters W and B of the logistic regression model, we need to define a cost function. Sigmoid(z) : [latex]z^{(i)} = w^Tx^{(i)} + b[/latex] Loss function : [latex]L(\hat{y}, y)[/latex] (measure how good our output [latex]\hat{y}[/latex] is when the true label is [latex]y[/latex]) Loss Function In Logistic Regression : [latex]L(\hat{y}, y) = -ylog(\hat{y}) - (1-y)log(1 - \hat{y})[/latex] (It measures how well you’re doing on a single training example) Cost Function : [latex]J(w,b) = \frac {1}{m} \sum_{i=1}^{m} L(\hat{y} ^{(i)}, y ^{(i)}) =\frac {1}{m} \sum_{i=1}^{m} (-y ^{(i)}log\hat{y} ^{(i)} - (1-y ^{(i)})log(1 - \hat{y} ^{(i)}))[/latex] (It measures how well you’re doing an entire training set)
Gradient Descent
Cost function J is a convex function
- Random initialization
- takes a step in the steepest downhill direction repeatedly [latex]\left\{\begin{matrix} w := w - \alpha \frac {\partial J(w,b)}{\partial w} \\ b := b - \alpha \frac {\partial J(w,b)}{\partial b} \end{matrix}\right.[/latex]
- converge to this global optimum or get to something close to the global optimum
Derivatives
Really all you need is an intuitive understanding of this in order to build and successfully apply these algorithms. Watch the videos and then if you could do the homework and complete the programming homework successfully then you can apply deep learning.
More Derivative Examples
- the derivative of the function just means the slope of a function and the slope of a function can be different at different points on the function
- if you want to look up the derivative of a function you can flip open your calculus textbook or look at Wikipedia and often get a formula for the slope of these functions at different points
Computation Graph
In order to compute derivatives Opa right to left pass like this kind of going in the opposite direction as the blue arrows that would be most natural for computing the derivatives so the recap the computation graph organizes a computation with this blue arrow left to right computation.
Derivatives with a Computation Graph
If you want to compute the derivative of this final output variable which uses variable you care most about, with respect to v, then we’re done sort of one step of backpropagation so the called one step backwards in this graph. By changing a you end up increasing v. Well, how much does v increase? It is increased by an amount that’s determined by dv/da and then the change in v will cause the value of J to also increase. So, in Calculus this is actually called the chain rule. A computation graph and how there’s a forward or left to right calculation to compute the cost functions. Do you might want to optimize. And a backwards or a right to left calculation to compute derivatives.
Logistic Regression Gradient Descent
How to compute derivatives for you to implement gradient descent for logistic regression. [latex]\frac{\mathrm{d} J}{\mathrm{d} u} = \frac{\mathrm{d} J}{\mathrm{d} v} \frac{\mathrm{d} v}{\mathrm{d} u} [/latex], [latex]\frac{\mathrm{d} J}{\mathrm{d} b} = \frac{\mathrm{d} J}{\mathrm{d} u} \frac{\mathrm{d} u}{\mathrm{d} b} [/latex], [latex]\frac{\mathrm{d} J}{\mathrm{d} a} = \frac{\mathrm{d} J}{\mathrm{d} u} \frac{\mathrm{d} u}{\mathrm{d} a} [/latex] Get you familiar with these ideas so that hopefully you’ll make a bit more sense when we talk about full fledged neural networks. Logistic Regression [latex]\left\{\begin{matrix} Lost \ Function : & L(\hat y^{(i)}, y^{(i)}) = -y^{(i)}log\hat y^{(i)} - (1-y^{(i)})log(1-\hat y^{(i)}) \\ Cost \ Function : & J(w,b) = \frac {1}{m} \sum _{i}^{m} L(\hat y^{(i)}, y^{(i)}) \end{matrix}\right.[/latex] Gredient Descent : [latex]\left\{\begin{matrix} w := w - \alpha \frac {\partial J(w,b)}{\partial w} \\ b := b - \alpha \frac {\partial J(w,b)}{\partial b} \end{matrix}\right.[/latex] Calculus : [latex]\frac{\mathrm{d} L(a,y)}{\mathrm{d} a} = -y/a + (1-y)/(1-a)[/latex] [latex]\left\{\begin{matrix} \frac{\mathrm{d} L(a,y)}{\mathrm{d} z} = \frac {\mathrm{d} L}{\mathrm{d} z} = \frac {\mathrm{d} L}{\mathrm{d} a} \frac {\mathrm{d} a}{\mathrm{d} z} \\ \frac {\mathrm{d} a}{\mathrm{d} z} = a \cdot (1-a) \\ \frac{\mathrm{d} L}{\mathrm{d} a} = -\frac{y}{a} + \frac{(1-y)}{(1-a)} \end{matrix}\right.[/latex] [latex]{\mathrm{d} z} = \frac{\mathrm{d} L(a,y)}{\mathrm{d} z} = \frac{\mathrm{d} L}{\mathrm{d} z} = (\frac {\mathrm{d} L}{\mathrm{d} a}) \cdot (\frac {\mathrm{d} a}{\mathrm{d} z} ) = (-\frac{y}{a} + \frac{(1-y)}{(1-a)}) \cdot a(1-a) = a - y[/latex] [latex]\left\{\begin{matrix} {\mathrm{d} w_1} = \frac {1}{m} \sum _i^m x_1^{(i)} (a^{(i)} - y^{(i)})\\ {\mathrm{d} w_2} = \frac {1}{m} \sum _i^m x_2^{(i)} (a^{(i)} - y^{(i)})\\ {\mathrm{d} b} = \frac {1}{m} \sum _i^m (a^{(i)} - y^{(i)}) \end{matrix}\right.[/latex]
Gradient Descent on m Examples
[latex]J(w,b) = \frac {1}{m}\sum _{i=1}^m L (a^{(i)}, y^{(i)})[/latex]
J=0;dw1=0;dw2=0;db=0;
for i = 1 to m
z(i) = wx(i)+b;
a(i) = sigmoid(z(i));
J += -[y(i)log(a(i))+(1-y(i))log(1-a(i));
dz(i) = a(i)-y(i);
dw1 += x1(i)dz(i);
dw2 += x2(i)dz(i);
db += dz(i);
J/= m;
dw1/= m;
dw2/= m;
db/= m;
w=w-alpha*dw
b=b-alpha*db
Vectorization
Vectorization is basically the art of getting rid of explicit for loops in your code. non-vectorized implementation :
z=0
for i in range(n_x)
z+=w[i]*x[i]
z+=b
vectorized implementation :
z=np.dot(w,x)+b
They’re sometimes called SIMD instructions. This stands for a single instruction multiple data. The rule of thumb to remember is whenever possible, avoid using explicit four loops.
More Examples of Vectorization
It’s not always possible to never use a for-loop, but when you can use a built in function or find some other way to compute whatever you need, you’ll often go faster than if you have an explicit for-loop.
Vectorizing Logistic Regression
How you can vectorize the implementation of logistic regression [latex]\left\{\begin{matrix} z^{(1)} = w^Tx^{(1)} + b \\ a^{(1)} = \sigma (z^{(1)}) \\ \hat y \end{matrix}\right.[/latex]
Z=np.dot(w.T, X)+b
It turns out, you can also use vectorization very efficiently to compute the backward propagation, to compute the gradients.
Vectorizing Logistic Regression’s Gradient
How you can use vectorization to also perform the gradient computations for all m training samples. [latex]\begin{matrix} Z = w^TX + b = np.dot(w.T, X) + b\\ A = \sigma (Z)\\ {\mathrm{d} Z} = A - Y\\ {\mathrm{d} w} = \frac {1}{m} * X * {\mathrm{d} z} ^T\\ {\mathrm{d} b} = \frac {1}{m} * np.sum({\mathrm{d} Z})\\ w := w - a * {\mathrm{d} w}\\ b := b - a * {\mathrm{d} b} \end{matrix} [/latex]
Broadcasting in Python
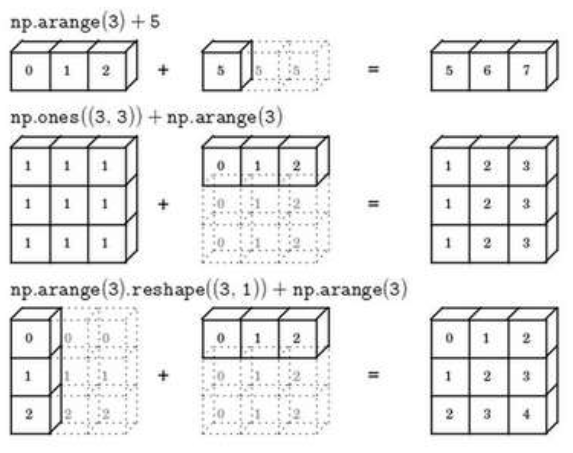
A note on python or numpy vectors
- Because with broadcasting and this great amount of flexibility, sometimes it’s possible you can introduce very subtle bugs very strange looking bugs.
- When you’re coding neural networks, that you just not use data structures where the shape is 5, or n, rank 1 array.
- Don’t hesitate to throw in assertion statements like this whenever you feel like it.
- Do not use these rank 1 arrays, you can reshape this.
Quick tour of Jupyter/iPython Notebooks
It’s so simple that nothing need to say.
Explanation of logistic regression cost function
A quick justification for why we like to use that cost function for logistic regression. [latex]\begin{matrix} \hat y = \sigma (w^Tx + b)\\ \sigma (z) = \sigma (w^Tx + b) = \frac {1}{1+e^{-z}}\\ \hat y = p(y = 1 x) \end{matrix}[/latex] [latex]\left.\begin{matrix} If \ y = 1 \ : & p(yx) = \hat y\\ If \ y = 0 \ : & p(yx) = 1 - \hat y \end{matrix}\right\} p(yx) = \hat y(1 - \hat y)^{(1-y)}[/latex] [latex]ylog\hat y + (1-y)log(1-\hat y)[/latex] In statistics, there’s a principle called the principle of maximum likelihood estimation, which just means to choose the parameters that maximizes this thing. Or in other words, that maximizes this thing. [latex]P(labels\ in\ training\ set) = \prod _{i=1}^{m} P(y^{(i)} x^{(i)})[/latex] [latex]logP(labels\ in\ training\ set) = log\prod _{i=1}^{m} P(y^{(i)} x^{(i)}) = \sum _{i=1}^{m}log P(y^{(i)} x^{(i)}) = \sum _{i=1}^{m} -L(\hat y^{(i)}, y^{(i)})[/latex] [latex]J(w,b) = \frac {1}{m} \sum _{i=1}^{m} L(\hat y^{(i)}, y^{(i)})[/latex]